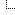Hey - weather was too nice, so was out playing hookie. Has teacher Marilyn vos Savant returned yet? No? TomK is still subbing? Ok, cool, cool - cake walk then.
So check it, let's work together before he comes back. He'll never know, right? Yeah, just add this to that vast list of stuff he doesn't know and stuff he doesn't know he doesn't know - he'll be none the wiser...
So you've read your Baysian Conditional Probability, right? Well here's the thing - to actually get an answer you need to know or ASSUME the prevalence x, but we can just work up the algebra and leave those little details for someone else to figure out. How hard can it be to make a test to find the prevalence of a disease that already requires knowing the prevalence of the disease?
So in general, if you have a population tested of D then you know the Total True Positives is D*x (population * prevalence) and the rest of the population is D - D*x. So for the 95% positive test the Test Positives that are True Positives is 0.95(D*x) and the Test Positives that are True Negatives are 0.05(D-D*x).
In this case we're just testing one person so D = 1 which simplifies the equations nicely.
So the overall probability that a Test Positive result is actually a True Positive is the True Positives divided by the Total Test Positives (True Positives and True Negatives), which is
0.95x / (0.95x + 0.05 * (1-x))
Here, someone check my work before teach gets back, I'll keep a look out.
https://ibb.co/6tsPZXM
So then, for 3% ASSUMED prevalence the math is:
0.95*0.03 / (0.95*0.03 +0.05 * (1-0.03))
=0.0285 / (0.0285 + 0.0485)
=0.0285 / 0.077 (hmm that number looks familiar)
=0.37 or 37%
So when you have a test with 5% error, and an ASSUMED 3% disease prevalence, you only have a 37% probability that a positive test result is actually a true positive.
Give it a try with a 5% ASSUMED prevalence while I step back out behind the toolshed for some enlightenment (Marilyn showed the testing is a joke) and flip some more coins.
Oh hey, substitute teacher TomK... Do you like apples? Well I got your number! How do you like them apples?
https://youtu.be/gcZPWkNY6x8?t=75
(with points to Reverend Bayes for figuring this all out centuries ago and apologies to the genius that is Matt Damon)
ETA: snark and spit wads